Graphs

Theory

A graph $G$ of order $o$ will be fully described by a square adjacency matrix $\mathcal{A}\in {\mathbb{M}}_{o\times o}(\mathbb{R})$ and a state vector $\mathcal{S}\in {\mathbb{R}}^o$.

$$G=\{\mathcal{A},\mathcal{S}\}$$

The adjacency matrix contains the weights $w(e_{i,j})$ of the edges (from the vertex $v_i$ to $v_j$ in this case). The particular case of $w(e_{i,j})=0$ indicates that their is no edge going from $v_i$ to $v_j$.

$${\mathcal{A}}_{i,j}=w(e_{i,j})$$

The state vector contains the states $s(v_i)$ of the vertices $v_i$.

$${\mathcal{S}}_i=s(v_i)$$

The neighborhood $N(v)$ of a vertex $v$ is the set of vertices which are adjacent to it. Thanks to the linear algebra description of graphs, there is a simple way to obtain a vector containing the weighted sum of the states present in the neighborhood of every vertex of a graph.

$$\begin{array}{r}\left(\begin{array}{c}\sum _{v_i\in N(v_1)}w(e_{1,i})\times s(v_i)\\ ⋮\\ \sum _{v_i\in N(v_o)}w(e_{o,i})\times s(v_i)\end{array}\right)=\left(\begin{array}{c}\sum _{i=1}^{o}w(e_{1,i})\times s(v_i)\\ ⋮\\ \sum _{i=1}^{o}w(e_{o,i})\times s(v_i)\end{array}\right)=\mathcal{A}\cdot \mathcal{S}\end{array}$$

We can also define the n-th neighborhood $N_n(v)$ of a vertex as the set of vertices which are at a distance $n$ of $v$.

Examples

The Graph class can be instantiated with two inputs: an adjacency matrix and a state vector both in the form of nested arrays.

import gra

graph = gra.Graph([ # adjacency matrix
        [0, 1, 1, 1],
        [1, 0, 1, 1],
        [1, 1, 0, 1],
        [1, 1, 1, 0] 
    ],[ # state vector
        [1],
        [0],
        [0],
        [0] 
    ])

Graph objects have three atributes:

• adjacency_matrix ( an instance of the SparseTensor class of TensorFlow )

• state_vector ( an instance of the Tensor class of TensorFlow )

• dtype ( a numpy data type object: np.int32 or np.float32 )

and eight methods:

• .plot(): plots the graph

• .evolve(rule): evolves the graph according the rule

• .order(): returns the order of the graph

• .diameter(): returns the diameter of the graph

• .clone(): returns a copy of the graph, this allows to use rules without modifying the original graph

• .to_igraph(): returns an igraph object

• .to_networkx(): returns a networkx object

• .to_mathematica(): returns a string corresponding to a Mathematica compatible version of the graph

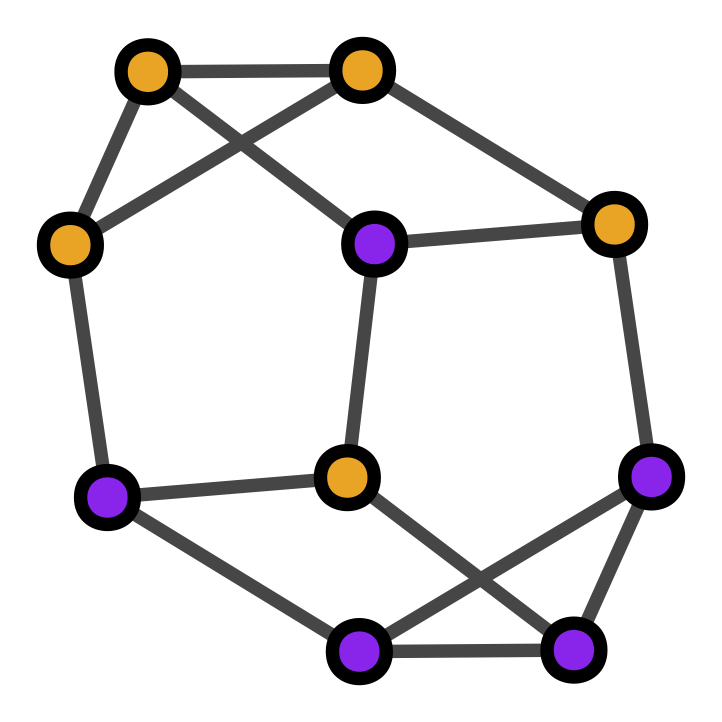
In the case of binary graphs $[s(v)\in \{0,1\}\mathrm{\forall }v]$, plots are such that:

• “alive” vertices $[s(v)=1]$ are colored purple,

• “dead” vertices $[s(v)=0]$ are colored orange.

graph.plot()

Graphs with a different ordering of vertices are equivalent. This equivalence can be checked with ==.

graph == gra.Graph([ # adjacency matrix
        [0, 1, 1, 1],
        [1, 0, 1, 1],
        [1, 1, 0, 1],
        [1, 1, 1, 0] 
    ],[ # state vector
        [0],
        [0],
        [1],
        [0] 
    ])

True